Regresión Logística – Práctica con Python
A continuación aprenderás a desarrollar un proyecto de Machine Learning enfocándonos en el algoritmo Regresión Logística. Cada una de las explicaciones dadas acá será paso a paso para que puedas entender con detalle cada uno de los métodos explicados acá y que los puedas implementar en tus propios proyectos.
Empecemos con la explicación del proyecto.
Definición del proyecto
En esta práctica del algoritmo de Regresión Logística, se desarrollará un modelo para predecir el cancer de seno.
Para este análisis vamos a utilizar el dataset disponible en la librería scikit-learn correspondiente al Breast Cancer o cáncer de seno. Si no lo sabías dentro de la librería sckit-learn se dispone de varios conjuntos de datos, muy básicos, con los que puedes practicar tus conocimientos de Machine Learning, no son muchos, pero cubre los principales tipos de algoritmos como regresión y clasificación.
El algoritmo específico que se utilizará será Regresión Logística.
Obtener los de datos
El primer paso que daremos será el de importar las librerías que vamos utilizar, en especial las necesarias para importar los datos que utilizaremos.
En este caso vamos a importar de sklearn el datasets, que es donde se guardan todos los conjuntos de datos que dispone esta librería.
#Se importan la librerias a utilizar
from sklearn import datasets
Ahora procedemos a importar los datos, para ello utilizamos la instrucción datasets punto load breast cancer y almacenamos esta información dentro de la variable dataset.
#Importamos los datos de la misma librería de scikit-learn
dataset = datasets.load_breast_cancer()
print(dataset)
Tenemos mucha información dentro de esta variable lo que se nos hace difícil entender la información, por lo tanto, ahora procedemos a entender la data.
Entender los datos
Para entender los datos que estaremos utilizando el proyecto nos vamos a valer de varias instrucciones propias de Python y así verificar la información contenida en el conjunto de datos que acabamos de importar. Para este fin utilizamos la instrucción keys.
print('Información en el dataset:')
print(dataset.keys())
Como podemos observar nos indica que el dataset cuenta con la siguiente información: primeramente “data”, que serían los datos independientes, seguidamente “target”, correspondiente a la columna con las etiquetas o respuestas, posteriormente tenemos “target_names” que son los nombres de las variables que se encuentran en la columna de “target”, después tenemos “DESCR” que sería la descripción total del dataset y finalmente tenemos “features_names” correspondiente a los nombres de cada una de las columnas de los datos.
Ya sabiendo todo esto podemos utilizar cada uno de estos nombres para entender mejor los datos, lo primero que vamos hacer es utilizar “DESCR” para conocer las características del dataset.
#Verificamos las características del dataset
print('Características del dataset:')
print(dataset.DESCR)
Aplicado el respectivo comando, podemos verificar que el dataset cuenta con 569 datos y un total de 30 atributos, todos ellos numéricos.
Algunos de los atributos o variables independientes son: el radio, la textura, el perímetro y el área, recuerda que acá vamos a predecir si un paciente tiene cáncer o no, para ello debemos conocer todas las características del tumor para determinar con ella si el tumor es maligno o benigno.
Podemos observar que de cada una de estas variables tenemos la información de la media, el error estándar y el peor, que vendría siendo la media de los tres valores más grandes.
Toda esta información hace los 30 atributos que en total cuenta este dataset.
Otro dato importante que nos proporciona esta información es que no existe ningún atributo perdido por lo que el dataset está completo haciendo que no sea necesario el preprocesamiento de los datos, para completar con datos perdidos.
Finalmente nos indica que en estos datos 212 son tumores malignos mientras que 357 son benignos, esto nos indica que los datos se encuentran balanceados por lo que no nos tenemos que preocupar por trabajar con un dataset desbalanceado.
Con esta información considero que ya tenemos más claro el dataset con el que estamos trabajando. En caso de que quieras profundizar en alguna información adicional puedes utilizar cualquiera de las otras instrucciones que he explicado en anteriores videos.
Ahora vamos a proceder a definir las variables de “X” y “y” que vamos emplear en nuestro modelo.
Procesamiento de los datos
Para “X” vamos a utilizar todas las variables que se encuentran dentro de “data”, por lo que la igualamos a dataset punto data.
#Seleccionamos todas las columnas
X = dataset.data
Por su parte, “y” será igual a los datos correspondientes a “target” por lo que igualamos esta variable a dataset punto target.
#Defino los datos correspondientes a las etiquetas
y = dataset.target
Recuerda que “y” cuenta con una sola columna con solamente ceros y unos, los unos indican que el tumor es maligno mientras que los ceros corresponden al tumor benigno.
Definido “X” y “y” ya podemos realizar la separación correspondiente a los datos de prueba y entrenamiento para ello importamos la respectiva librería y procedemos a utilizar train_test_split para separar los datos.
Para la separación de los datos, vamos a tomar un 20% de los mismos para utilizarlos como prueba una vez que hayamos obtenido el modelo.
from sklearn.model_selection import train_test_split
#Separo los datos de "train" en entrenamiento y prueba para probar los algoritmos
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
El siguiente paso que realizaremos es escalar los datos, esto se hace ya que las características son completamente distintas en magnitudes, unidades y rango por lo que lo mejor es escalarlos para llevarlos a un mismo nivel de magnitudes.
Para realizar este procedimiento importaremos el método StandarScaler de la librería scikit-learn.
#Se escalan todos los datos
from sklearn.preprocessing import StandardScaler
Seguidamente igualamos la variable escalar a “StandardScaler” para que lo podamos implementar con nuestros datos.
Para realizar este procedimiento importamos el método StandardScaler de la librería scikit-learn.
escalar = StandardScaler()
Realizado todo ahora si podemos escalar los datos, para nuestro caso los datos a escalar son lo que tenemos dentro de las variables “X” tanto de entrenamiento como de prueba.
Ahora para realizar el escalamiento utilizaremos fit_transform, esta instrucción realiza el calculo respectivo y a su vez transforma y devuelve los datos ya escalados.
X_train = escalar.fit_transform(X_train)
X_test = escalar.transform(X_test)
Ya en este momento tenemos nuestros datos listos para empezar a construir el modelo.
Desarrollo del algoritmo
Lo primero que debemos hacer es importar LogisticRegression que se encuentra dentro de la librería linear_model, y a su vez definimos el algoritmo.
#Definimos el algoritmo a utilizar
from sklearn.linear_model import LogisticRegression
algoritmo = LogisticRegression()
Seguidamente entrenamos el modelo utilizando la instrucción fit y los datos tanto de “X” como de “y” de entrenamiento.
#Entrenamos el modelo
algoritmo.fit(X_train, y_train)
Y finalmente realizamos una predicción, utilizando la instrucción predict y los datos de prueba.
#Realizamos una predicción
y_pred = algoritmo.predict(X_test)
Análisis de los resultados
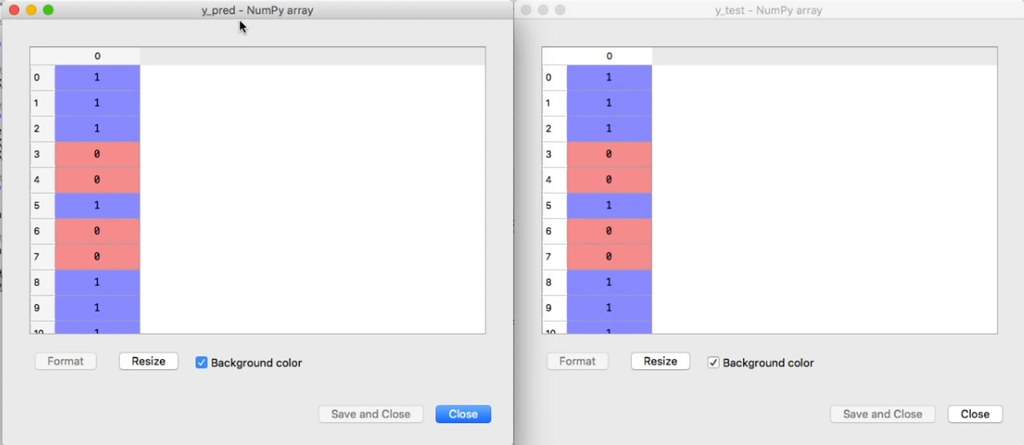
Si comparamos los datos que predecimos con los datos reales podemos ver que nuestro modelo realizo un excelente trabajo ya que a simple vista podemos observar que los datos predichos son exactamente igual a los datos reales.
Los datos predichos son los ubicados en la tabla de lado izquierdo mientras que los originales se encuentran en el lado derecho.
Pero veamos si esto es cierto, para ello calculamos las métricas respectivas para verificar el rendimiento del modelo. Para esto debemos primero obtener la matriz de confusión utilizando la librería metrics de scikit learn y el módulo confusion-matrix.
#Verifico la matriz de Confusión
from sklearn.metrics import confusion_matrix
matriz = confusion_matrix(y_test, y_pred)
print('Matriz de Confusión:')
print(matriz)
La matriz nos indica que cuenta con 39 datos verdaderos positivos, es decir datos que en los datos reales eran 1 y el modelo los predijo correctamente.
Por su parte son 71 los datos verdaderos negativos, esto quiere decir datos reales que eran 0 y el modelo los predijo como tal.
Veamos ahora la cantidad de datos que el modelo no predijo correctamente. Comencemos con los datos falsos negativos, en total fueron 3, esto quiere decir datos reales que eran 1 pero el modelo los predijo como 0.
En cuanto a los datos falsos positivos fue solamente 1 solo dato, que era en realidad 0 y el modelo lo predijo como 1.
La matriz de confusión nos indica que solamente fueron 4 datos los que el modelo no predijo correctamente, pero con el resto de los datos si lo hizo de manera correcta. Recuerda que acá solamente estamos evaluando el conjunto de datos de pruebas que representa solamente un 20% de nuestros datos.
Calculemos ahora todas las métricas que podemos evaluar para los modelos de clasificación.
A pesar de que este dataset se encuentra balanceado y que calculando solamente la precisión del modelo podemos evaluar de manera correcta el rendimiento del mismo, les voy a explicar cómo obtener el resto de métricas en caso de que estés trabajando con algún conjunto de datos desbalanceado.
Comencemos entonces calculando la precisión del algoritmo para ello utilizamos la librería metrics de scikit-learn e importamos precision_score, y la implementamos junto con los datos reales y los que hemos obtenidos utilizando el modelo.
#Calculo la precisión del modelo
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred)
print('Precisión del modelo:')
print(precision)
El resultado de la precisión es de 0,959.
Esto coincide con lo que vimos en la matriz de confusión, demostrando que nuestro modelo es bastante bueno.
Calculemos ahora la exactitud del modelo, por lo que debemos ahora importar accuracy_score, de la misma librería de metrics.
#Calculo la exactitud del modelo
from sklearn.metrics import accuracy_score
exactitud = accuracy_score(y_test, y_pred)
print('Exactitud del modelo:')
print(exactitud)
Aplicamos este comando a los datos de pruebas y obtenemos una exactitud de 0,964, valor muy parecido al anterior.
Veamos ahora la sensibilidad o lo que también se le conoce como recall del algoritmo, para ello importamos recall_score.
#Calculo la sensibilidad del modelo
from sklearn.metrics import recall_score
sensibilidad = recall_score(y_test, y_pred)
print('Sensibilidad del modelo:')
print(sensibilidad)
Implementando esta métrica obtenemos una sensibilidad del 0,986.
Calculemos ahora el puntaje F1 que es una combinación entre la precisión y la sensibilidad, para esto importamos f1_score.
#Calculo el Puntaje F1 del modelo
from sklearn.metrics import f1_score
puntajef1 = f1_score(y_test, y_pred)
print('Puntaje F1 del modelo:')
print(puntajef1)
Realizado esto procedemos a implementar la instrucción junto a los datos calculados del modelo, obteniendo 0,972.
Finalmente, la curva ROC – ACU del modelo, para ello importamos roc_auc_score. Recuerda que todas estas instrucciones se encuentran dentro de la librería scikit-learn dentro de metrics.
#Calculo la curva ROC - AUC del modelo
from sklearn.metrics import roc_auc_score
roc_auc = roc_auc_score(y_test, y_pred)
print('Curva ROC - AUC del modelo:')
print(roc_auc)
Aclarado esto implementamos el comando junto con los datos respectivos y obtenemos 0,957.
Verificando todos los datos obtenidos vemos que son similares unos y otros.
Recuerda que no es necesario hacer todos estos cálculos porque nuestros datos se encuentran balanceados, los hago acá para que vean cómo se pueden obtener.
Programa completo
A continuación se encuentra el código completo:
"""
Regresión Logística
"""
########## LIBRERÍAS A UTILIZAR ##########
#Se importan la librerias a utilizar
from sklearn import datasets
########## PREPARAR LA DATA ##########
#Importamos los datos de la misma librería de scikit-learn
dataset = datasets.load_breast_cancer()
print(dataset)
########## ENTENDIMIENTO DE LA DATA ##########
#Verifico la información contenida en el dataset
print('Información en el dataset:')
print(dataset.keys())
print()
#Verifico las características del dataset
print('Características del dataset:')
print(dataset.DESCR)
#Seleccionamos todas las columnas
X = dataset.data
#Defino los datos correspondientes a las etiquetas
y = dataset.target
########## IMPLEMENTACIÓN DE REGRESIÓN LOGÍSTICA ##########
from sklearn.model_selection import train_test_split
#Separo los datos de "train" en entrenamiento y prueba para probar los algoritmos
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
#Se escalan todos los datos
from sklearn.preprocessing import StandardScaler
escalar = StandardScaler()
X_train = escalar.fit_transform(X_train)
X_test = escalar.transform(X_test)
#Defino el algoritmo a utilizar
from sklearn.linear_model import LogisticRegression
algoritmo = LogisticRegression()
#Entreno el modelo
algoritmo.fit(X_train, y_train)
#Realizo una predicción
y_pred = algoritmo.predict(X_test)
#Verifico la matriz de Confusión
from sklearn.metrics import confusion_matrix
matriz = confusion_matrix(y_test, y_pred)
print('Matriz de Confusión:')
print(matriz)
#Calculo la precisión del modelo
from sklearn.metrics import precision_score
precision = precision_score(y_test, y_pred)
print('Precisión del modelo:')
print(precision)
#Calculo la exactitud del modelo
from sklearn.metrics import accuracy_score
exactitud = accuracy_score(y_test, y_pred)
print('Exactitud del modelo:')
print(exactitud)
#Calculo la sensibilidad del modelo
from sklearn.metrics import recall_score
sensibilidad = recall_score(y_test, y_pred)
print('Sensibilidad del modelo:')
print(sensibilidad)
#Calculo el Puntaje F1 del modelo
from sklearn.metrics import f1_score
puntajef1 = f1_score(y_test, y_pred)
print('Puntaje F1 del modelo:')
print(puntajef1)
#Calculo la curva ROC - AUC del modelo
from sklearn.metrics import roc_auc_score
roc_auc = roc_auc_score(y_test, y_pred)
print('Curva ROC - AUC del modelo:')
print(roc_auc)
print('Precisión del modelo:', precision)
print('Exactitud del modelo:', exactitud)
print('Sensibilidad del modelo:', sensibilidad)
print('Puntaje F1 del modelo:', puntajef1)
print('Curva ROC - AUC del modelo:', roc_auc)
Si te llamo la atención todo este contenido y te animaste a empezar a estudiar Inteligencia Artificial, he desarrollado un curso que te ayudará, de igual forma a iniciar tu camino dentro de está tecnología. Este curso te sentará las bases y te dará más claridad para poder seleccionar el enfoque o área que más te interese sobre la Inteligencia Artificial, de igual forma te ayudará tener más claridad en muchos conceptos que seguramente en estos momentos te parece confusos. Este curso es ideal si apenas estás empezando. Si quieres más información puedes ingresar a este enlace.
POR QUE UTILIZA LA PREDICION PARA CALCULAR roc_auc , Y NO UTILIZA LA PREDIC_PROBA ?
DEBERIA UTILIZAR PREDIC_PROBA
roc_auc = roc_auc_score(y_test, y_pred)
print(‘Curva ROC – AUC del modelo:’)
print(roc_auc)